Нечеткая Марковская цепь является одной из моделей неопределенности, в которой сочетаются случайность и нечеткость, что в свою очередь приводит к появлению понятия нечеткой вероятности. В классической теории вероятность есть детерминированная характеристика возможности появления событий в определенных условиях. Вместе с тем, в реальной жизни эта возможность может неконтролируемым образом зависеть от совокупности условий, которые сами могут измениться. В этих случаях вероятность естественно описывать нечетким числом с функцией принадлежности, параметры которой оцениваются статистически по совокупности испытаний [1]. Нечеткие Марковские процессы с дискретными состояниями удобно представлять и иллюстрировать с помощью нечеткой переходной матрицы и нечеткого графа состояний системы, поскольку система может прибывать в одном из n состояний и для каждого момента времени t необходимо задать n2 вероятностей перехода Pij [2-4].
В данной работе мы предлагаем рассмотрение представления однородных нечетких целей Маркова в виде нечеткой переходной матрицы состояний с привлечением аппарата нечеткой математики. Предлагается математическая модель однородной нечеткой цепи Маркова на примере, который рассматривает процесс функционирования системы автомобиля в условиях неопределенности. Нечеткий случайный процесс будем называть нечеткой Марковской цепью, если для каждого k-го шага случайная последовательность событий (состояний) S(0),S(1),…,S(k) и нечеткая вероятность перехода из любого состояния Si в любое Sj не зависит от того, когда и как система пришла в состояние Sj. Начальное состояние S(0) может быть заданным заранее или случайным образом. Нечеткие вероятности цепи Маркова будем называть вероятности Pi(k) того, что после k-того шага (и до (k+1)-го) система S будет находиться в состояние Si (i = 1,2,…,n). Очевидно, что для любого k:
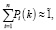(1)
где Pi(k) – нечеткие числа, 1� – нечеткая единица, модальное значение которой равно 1.
Если начальное состояние системы S в точности известно S(0) = Si, то начальная вероятность Pi(0) = 1, а все остальные равны нулю.
Нечеткой вероятностью перехода (переходной вероятностью) на k-ом шаге из состояния Si в состояние Sj будем называть нечеткую условную вероятность того, что система S после k-го шага окажется в состоянии Sj при условии, что непосредственно перед этим (после (k–1)-го шага) она находилась в состоянии Si.
Поскольку система может пребывать в одном из n состояний, то для каждого момента времени t необходимо задать n2 нечетких вероятностей перехода Pij, которые удобно представить в виде следующей нечеткой матрицы:
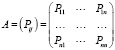, (2)
где Pij – нечеткая вероятность перехода за один шаг из состояния Si в состояние Sj; Pij – нечеткая вероятность задержки в состояние Sj. Здесь Pij являются нечеткими гауссовыми числами с соответствующими функциями принадлежности:
,
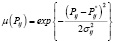где Pijº – модальное значение (ядра) нечетких чисел;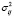 
– коэффициенты концентрации (носители). Матрица (2) называется нечеткой переходной или матрицей нечетких переходных вероятностей [2-4].
Если нечеткие переходные вероятности не зависят от номера шага (от времени), а зависят только от того, из какого состояния в какое осуществляется переход, то соответствующая нечеткая Марковская цепь называется однородной.
Если для нечеткой однородной Марковской цепи заданы нечеткое начальное распределение переходимых вероятностей (Pij), то нечеткие вероятности состояний системы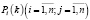 
определяюся рекуррентной формулой [2]:
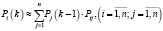(3)
с соответствующими функциями принадлежности компонентов нечеткого решения задачи (3)
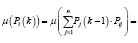
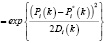, (4)
,
.
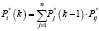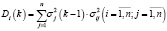Построим математическую модель однородной нечеткой цепи Маркова на примере, который рассматривает процесс функционирования системы автомобиля в условиях неопределенности.
Пример. Рассмотрим процесс функционирования системы автомобиля в условиях неопределенности. Пусть автомобиль (система) в течение одной смены (суток) находится в одном из двух состояний: исправном (состояние-1) и неисправном (состояние-2). Опыт эксплуатации этого автомобиля свидетельствует о том, что для него имеет место матрица нечетких переходных вероятностей, соответствующая состояниям: исправен (состояние-1) и неисправен (состояние-2):
,
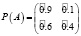где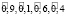 
– нечеткие гауссовы числа с соответствующими функциями принадлежности
,
,
,
;
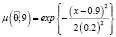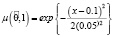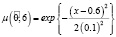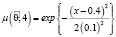где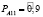 
– нечеткая вероятность того, что автомобиль находится в исправном состоянии, 
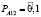– нечеткая вероятность перехода автомобиля из состояния «исправен» в состояние «неисправен», 
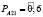– нечеткая вероятность перехода автомобиля из состояния «неисправен» в состояние «исправен», 
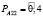– нечеткая вероятность того, что автомобиль останется в состоянии «неисправен».
Нечеткие элементы матрицы перехода определены за трехнедельный период эксплуатации автомобиля.
Требуется определить нечеткие вероятности состояний автомобиля через двое суток эксплуатации, если в начальном состоянии вектор начальных вероятностей состояния автомобиля задан (P1(0) = 1, P2(0) = 0)
Решение. Используя матрицу нечетких переходных вероятностей, определим нечеткие вероятности состояний Pi(k) после первого шага (после первых суток эксплуатации автомобиля) по формулам (3)-(4):
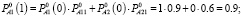
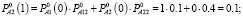
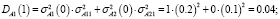
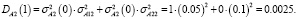
Таким образом, после первых суток эксплуатации, автомобиль будет находиться в состоянии-1 с нечеткой вероятностью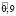 
и в состоянии-2 с вероятностью 
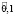с соответствующими функциями принадлежности:
, 
.
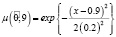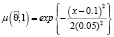Определим нечеткие вероятности состояний после вторых суток эксплуатации автомобиля:
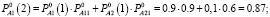
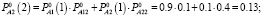
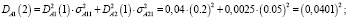
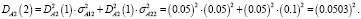
Таким образом, после вторых суток эксплуатации, автомобиль будет находиться в состоянии-1 с нечеткой вероятностью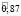 
и в состоянии-2 с вероятностью 
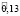с соответствующими функциями принадлежности:
, 
.
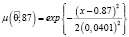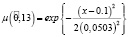В данной работе представлено рассмотрение основных понятий теории однородных нечетких цепей Маркова с привлечением нечеткой математики. Построена математическая модель однородной нечеткой цепи Маркова на примере, в котором рассмотрен процесс функционирования системы автомобиля в условиях неопределенности (нечеткости).
Библиографическая ссылка
Антоненко А.С., Барышевский С.О. ОДНОРОДНЫЕ НЕЧЕТКИЕ ЦЕПИ МАРКОВА // Материалы МСНК "Студенческий научный форум 2025". 2023. № 15. С. 81-83;URL: https://publish2020.scienceforum.ru/ru/article/view?id=798 (дата обращения: 04.04.2025).