В существующих условиях наблюдается развитие систем связи. Формируются методики по расчету сложных дифракционных объектов.
Наблюдения показывают, что создание радиолокационных компонентов за последние несколько лет существенным образом усложнилось. Обусловлено это тем, что увеличились требования относительно технических характеристик подобных объектов. Они связаны с увеличением дальности обнаружения объектов, того, как быстро они будут идентифицированы [1]. Существуют большие углы обзора и др. При этом требуется знание совокупности тонких характеристик рассеивающих компонентов и антенных компонентов. Среди них можно отметить уровень кросс-поляризационных излучений, характеристики фазовых диаграмм направленности. Еще есть влияние уровней боковых, а также задних лепестков в амплитудных диаграммах направленности (ДН). Весьма актуальна подобная задача по объектам сложной формы при больших электрических размерах.
При формировании современных радиолокационных компонентов важно вести совершенствование средств по их проектированию. При этом одним из ключевых вопросов можно считать проведение моделирования функционирования базовых составляющих дифракционных структур. Это относится к широкому диапазону необходимых характеристик. Необходимо рассчитывать характеристики рассеяния антенн, которые будут отвечать современным требованиям. В ходе моделирования есть возможности построения методик и алгоритмов прогнозирования характеристик рассеяния радиоволн [2,3].
Необходимо построить модель прогнозирования. На ее базе будут возможности для того, чтобы получать информацию относительно возможных состояний объектов прогнозирования [4, 5].
Простейшие методы по восстановлению применяемых в ходе прогнозирования зависимостей, основываются на заданном временном ряде, т. е. функции, которая определена для конечного числе точек на оси времени.
Многомерная регрессия, это касается и использования непараметрических оценок плотности распределений – является основным в существующих условиях статистическим аппаратом для проведения прогнозирования.
К современным статистическим подходам прогнозирования относятся также модели авторегрессии, модель Бокса-Дженкинса, системы эконометрических уравнений, основанные как на параметрических, так и на непараметрических подходах.
Качественные основываются на рассмотрении существующих опыта, знаний и интуиции исследователей. Весьма большое распространение в подобной группе имеют методы экспертных оценок. Сущность метода состоит в том, что прогнозные оценки определяются на основе заключений экспертов, которым поручается аргументированное обоснование своего мнения о состоянии и развитии того или иного рынка либо проблемы. Методы экспертных оценок, как правило, имеют качественный характер.
Основными процедурами обработки прогностических экспертных оценок являются проверка согласованности, кластер-анализ и нахождение группового мнения.
Объектом нашего исследования будет рассеяние на двумерном идеально проводящем цилиндре с длиной L и радиусом a.
Мы будем рассматривать случай линейного процесса рассеяния электромагнитных волн. Кроме того, мы будем полагать, что функция рассеяния объекта описывает линейную зависимость между падающим и рассеянным полем. Зависимость, которая определяет, то, как связаны линейно комплексные амплитуды напряженностей рассеянного Es(r) и облучающего Ei(r) на контуре рассматриваемого цилиндра P, такая:
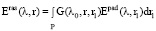, (1)
здесь l, l0 ∈ [l1, l2], G(l0, r, r1) – является пространственной импульсной переходной функцией объекта (РЛХ). Она соответствует длине волны l0. Ее мы предполагаем постоянной для диапазона длин волн [l1, l2].
Функцию G мы рассчитываем, как:
G = GL = Eras / Epad,
где Eras – рассеянное поле, Epad – падающее поле.
Прогнозирование по характеристикам рассеяния мы вели по углам наблюдения q∈[0°, qmax]. При этом угол qmax мы выбирали в ходе анализа конкретного компонента. Мы оценивали функцию G базируясь на том, что мы знаем ее значение по нескольким значениям размеров L цилиндра так:
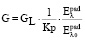, (2)
здесь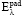 
– это первичная волна для длины волны l, 
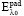– первичная волна на длине волны l0, GL вычисляется на длине волны l0, Kp – коэффициент. Коэффициент Kp выбирается с целью получения лучших результатов прогнозирования. Для размера объекта L коэффициент Kp выбирается равным 1. Используя теорему о свертке, а также рассматривая предположение о постоянстве y на интервале [l1, l2], имеем следующее выражение:
SS(w, l) = S(w) × S0(w, l), (3)
где введены такие обозначении, как SS, S, S0, показывающие преобразования Фурье для функций Eras, y, Epad по пространственным частотам w. Указанную модель мы анализировали в диапазоне длин волн [l1, l2]. Изучали длину волны l0, на которой рассчитывается функция S(w). Для выбранных нами значений lk ∈ [l1, l2] были определены диаграммы рассеяния. Разница среди рассчитанной и прогнозируемой характеристикой не должна превышать 2,5 дБ. Угол qmax мы выбрали 90°. Тогда прогнозирование осуществлялось по углам наблюдения q ∈ [0°, 90°]. Зная двумерную ЭПР двумерного цилиндра, существует возможность найти трехмерную ЭПР цилиндра прямоугольного поперечного сечения. Расчет точных значений характеристик рассеяния для двумерной модели цилиндра был осуществлен на основе решения интегрального уравнения первого рода для случая E-поляризации падающей электромагнитной волны. Для демонстрации работоспособности методики расчеты проводились для случая равенства размеров высоты и длины цилиндра a = H.
Представляет интерес развивать рассмотренные подходы для других объектов. Использование указанных подходов в совокупности с другими методиками дает возможность комплексного исследования объектов.