В статье рассматривается ФГОС НОО второго поколения о форме логического мышления, в том числе формы логического мышления как универсальное учебное действие (УУД). Введение понятий в начальной школе как один из методических приёмов развития логического мышления. Также способы введения понятий на уроках математики в разных учебно-методических комплексах и требования к определению понятий.
Логическое мышление представляет собой процесс, при котором используются логические понятия человеком, которому присуще рассудительность, доказательность, а его целью является получение обоснованных выводов из существующих предпосылок. Умение логически мыслить – это умение верно строить суждения, анализировать их и делать верные выводы. Без этого умения младшему школьнику нельзя обойтись как на уроке, так и в повседневной жизни. Несмотря на то, что формирование и развитие логических умений трудоёмкий процесс, он необходим для всестороннего развития ребёнка. ФГОС НОО второго поколения рассматривает формирование логического мышления, как универсальное учебное действие [1]. Развитие логического мышления происходит на разных предметах, изучаемых учащимися в начальной школе. Особая роль в этом процессе принадлежит математике, так как она обладает всем необходимым инструментарием. Развитие логического мышления предполагает овладение логическими действиями: классификации по родовидовым признакам, установление причинно-следственных связей, построение рассуждений, оперирование понятиями, а также алгоритмического мышления [2]. На уроках математики у учащихся происходит: формирование понятий и способов их определения, овладение правилами логического вывода, понимание и сохранение в памяти способов построения рассуждений. Умению рассуждать, классифицировать, обобщать и анализировать способствуют все разделы, изучаемые в курсе математики начальной школы. Полученные в начальной школе представления о понятиях служат твёрдым фундаментом для дальнейшего изучения математики.
Для формирования математических понятий необходимо понимание математического объекта, который в понятии характеризуется благодаря применению определенных умственных действий. Математика изучает окружающий нас мир, природные и общественные явления, но изучает лишь особые стороны этих явлений [3, с.8]. Рассмотрим задачу, в которой нужно рассчитать, сколько рулонов обои необходимо купить для облицовки стены, если известно, что размер обойного рулона – 10,05 м длины на 0,53 м ширины. В данной ситуации не имеет значения, из чего изготовлена или какого цвета стена. Следует знать лишь форму и размер этой стены. В этом случае исключаем все свойства рассматриваемого предмета и выделяем только его размер и форму. Вследствие такого отвлечения получаем геометрическую фигуру, которая является математическим объектом.
Математические объекты – это результат выделения из предметов и явлений окружающего мира особых количественных и пространственных свойств и отношений, и абстрагирования от всех других свойств [3, с.8]. Следовательно, математические объекты не существуют в реальной жизни. Вследствие этого говорят, что идеальными объектами, описывающие реальные объекты, являются математические объекты. Все математические объекты обладают какими-то признаками.
Признаки – это отличительные и схожие показатели одного объекта от другого, благодаря этому можно узнать, определить и описать объект.
Каждый объект в окружающем нас мире обладает существенными и несущественными признаками. Существенный признак – показатели, принадлежащие объекту при целых условиях, без которого данный объект существовать не может. В несущественном же признаке, отсутствие показателей не влияет на существование объекта.
Таким образом, понятие – это целостная совокупность суждений о существенных признаках соответствующего объекта [4].
Понятие – форма мышления, в которой выделяются и обобщаются предметы того или иного класса по существенным отличительным признакам [4, с.15].
При изучении математического объекта, используется действие определение для получения понятия о нём.
Определение – это предложение, с помощью которого раскрывается содержание понятия или устанавливается значение термина [3, с.15]
Для определения понятия необходимо выбрать существенные признаки объекта, при которых можно будет отличить его от других.
Определения различают на вербальные и невербальные определения [5].
Невербальное определение – это определение понятия путем непосредственной демонстрации объектов, охватываемых этим понятием, или приведение контекста, в котором содержится то или иное понятие [3, с.16]. К невербальному определению относится остенсивное – устанавливает значение терминов путем демонстрации объектов, которые этим термином определяются [3, с.14]. С использованием такого определения в начальной школе вводится понятие «числовое выражение», «числовое равенство», «угол» и т.д. Покажем это на примере понятия прямого угла. В учебнике по математике для 2 класса Ассоциация 21 век «Гармония» (авт. Истомина Н.Б.) предлагается задание:
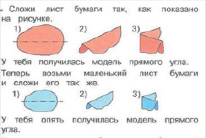
Рис. 1. Понятие прямого угла. УМК «Гармония»
Также в учебнике по математике для 2 класса УМК «Школа России» (авт. М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова) предлагается задание:
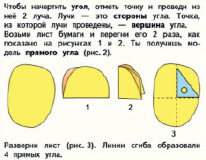
Рис. 2. Понятие прямого угла. УМК «Школа России»
Контекстуальные определения – содержание понятия раскрывается через некоторый контекст [3, с.17]. Например, понятие буквенных выражений в учебнике математики для 4 класса Ассоциация 21 век «Гармония» (авт. Истомина Н.Б.) вводится контекстуально. Смысл действия буквенных выражений раскрывается с помощью рисунка и специально сконструированного текста.

Рис. 3. Буквенные выражения. УМК «Гармония»
В учебнике математики для 2 класса (УМК «Школа России, 2 класс, ч.1, авт. М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова) представлено так:

Рис. 4. Введение буквенного выражения в УМК «Школа России»
Рассмотрим некоторые способы вербальных определений.
1) Определение понятий через род и видовое отличие. При определении какого-либо предмета указывают на ближайшее родовое понятие, в объёме которого мыслится определяемый предмет, и называют его отличительный признак [5]. Такие определения имеют схему: вид = род + видовое отличие. Например, «Квадрат – это прямоугольник, у которого все стороны равны». Вид –квадрат. Род – прямоугольник. Видовые отличия: все стороны равны. Например, в учебнике математики для 2 класса (УМК «Школа России, 2 класс, авт. М.И. Моро и др.:
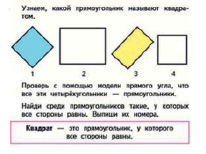
Рис. 5. Понятие квадрат. УМК «Школа России»
2) Генетическое определение понятий. Описание характерного для определяемого предмета способа образования или способа происхождения. Например, в учебнике математики для 3 класса (УМК «Школа России, 3 класс, авт. М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова) понятие окружности вводится по способу образования:

Рис. 6. Понятие окружности. УМК «Школа России»
3) В рекурсивных определениях указываются некоторые основные элементы из объема понятия и даются правила, позволяющие получить новые элементы из уже имеющихся [3, с.18]. Например, в учебнике математики для 2 класса (УМК «Школа России, 2 класс, ч.2, авт. М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова, С.В. Степанова) понятие острого и тупого угла вводится сравнением через показ:
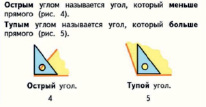
Рис. 7. Понятие острого и тупого угла. УМК «Школа России»
Требования к определению понятий:
– определение должно содержать указание на ближайшее родовое понятие.
– определения не должны содержать «порочного круга». В его определяющей части не должен содержится определяемый термин
– определение не должно быть тавтологией, т.е. повторять в иной словесной форме ранее сказанное;
– определение должно быть достаточным;
– определение не должно быть избыточным.
При формировании понятий, учителю принадлежит ведущая роль. Так, для определения понятий круг и окружность, площадь фигуры и его периметр, учитель должен сформировать у учащихся понятие о геометрической фигуре и её границе. Если учитель не сделает это, то учащиеся среднего звена будут допускать ошибки при нахождениях таких величин как «площадь» и «периметр».

