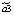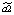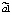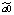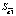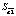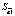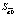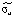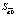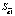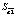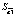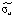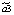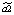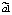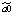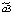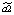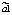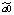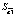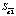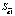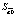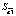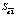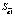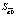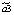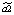В статье представлено исследование, касаемое влияния различных факторов на динамику оборота розничной торговли, выявлена социально-экономическая значимость изучения данного показателя. В работе проведен эконометрический анализ динамики оборота розничной торговли за 2015-2019 гг., построена качественная модель множественной регрессии. Полученная модель может быть использована для оценки социально-экономической ситуации в стране, дальнейшего ее прогнозирования.
Показатель оборота розничной торговли является одним из важнейших индикаторов состояния экономики страны или отдельных ее регионов. Его увеличение говорит о росте прибыли торгующих организаций, что в свою очередь подразумевает увеличение поступлений денежных средств в региональный и федеральный бюджет в качестве налога на прибыль. Также увеличение показателя оборота розничной торговли подразумевает развитие сетей розничной торговли, следовательно, появление новых рабочих мест, рост национального благосостояния.
Тем самым, показатель оборота розничной торговли имеет особое экономическое значение, а проблема исследования факторов, влияющих на его динамику, имеет значительную актуальность в настоящее время, так как помогает исследовать возможные пути улучшения данного показателя и соответственно пути роста экономического потенциала страны.
Целью данной работы является изучение и построение качественной эконометрической модели динамики оборота розничной торговли.
Для выполнения поставленной цели предполагается осуществить решение следующих задач: изучить экономическую суть показателя оборота розничной торговли; провести анализ факторов, влияющих на данный показатель; построить эконометрическую модель, что в свою очередь включает в себя несколько этапов: построение спецификации, сбор статистической информации, вычисление и оценка параметров модели, проверка ее на адекватность.
В качестве объекта исследования выступает динамика оборота розничной торговли.
Предметом же исследования являются факторы, влияющие на оборот розничной торговли.
Существует огромное количество факторов, влияющих на динамику оборота розничной торговли. Но все они в разной степени оказывают влияние на формирование конечного результата [1].
В данной работе представлена спецификация модели в виде линейной множественной регрессии:
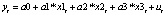
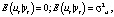
где yt – динамика оборота розничной торговли в % к предыдущему году; x1t – динамика среднемесячной номинальной заработной платы работников организации в % к предыдущему году; x2t – индекс потребительских цен (ИПЦ) в % к предыдущему году; x3t – динамика среднемесячного объема импорта в % к предыдущему периоду; a0 – автономный уровень динамики оборота розничной торговли, не зависящий от регрессоров; a1; a2; a3 – соответствующие параметры переменных; ut – случайный остаток – степень влияния на объясняемую переменную неучтенных факторов.
Временной промежуток для исследуемых данных был взят с начала 2015 года (январь) по конец 2019 года (декабрь) [2].
Таблица 1
Корреляционная таблица
|
Об. Розн. Торг |
ЗП |
ИПЦ |
Имп |
|
|
Об. Розн. Торг. |
1 |
|||
|
ЗП |
0,886205 |
1 |
||
|
ИПЦ |
-0,42256 |
-0,22878 |
1 |
|
|
Имп |
0,736187 |
0,613784 |
-0,36106 |
1 |
Источник: составлено автором.
При построении корреляционной таблицы учитывались динамика заработной платы, ИПЦ и импорта, можно заметить отсутствие мультиколлиниарности в модели. Стоит отметить, что при удалении ИПЦ из спецификации, скорректированный R^2 уменьшается почти на 3 %, что говорит о том, что данный регрессор должен присутствовать в модели.
Таблица 2
Оценки параметров модели линейной регрессии.
|
|
|
|
|
R^2 = 0,871 |
|
0,173 |
-2,991 |
0,584 |
324,020 |
|
|
|
|
|
|
|
|
0,044 |
0,882 |
0,051 |
90,000 |
|
|
|
||||
|
3,72 |
||||
Источник: составлено автором.
Оцененный вид модели:
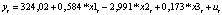
|
|
|
|
|
|
|
90,000 |
0,051 |
0,882 |
0,044 |
3,72 |
Стандартные ошибки оценённых коэффициентов на порядок ниже самих оценённых коэффициентов, что может говорить о высокой точности полученных оценок.
Анализ проверки спецификации на ошибки в построении подтвердил их отсутствие. Так, 1-й вид ошибки заключается в ошибочном виде типа спецификации, первый симптом которой – несоответствие диаграммы рассеяния графику функции.

Диаграмма рассеяния. Источник: составлено автором
Так как в модели несколько регрессоров по графику функции сложно оценить наличие данного симптома. Если наблюдать зависимость наблюдаемой переменной от каждой объясняющей, можно заметить линейный тренд (рисунок).
Второй симптом ошибки – длительное постоянство знака случайных остатков в упорядоченном виде по возрастанию значений сумм модулей объясняющих переменных уравнений наблюдений. Стоит отметить, что знакопостоянство отсутствует на длительных промежутках времени, оно продолжается максимум для 4 идущих подряд ut, что составляет 4/60 = 0,067 или 6,7 % < 10 %. Это говорит об отсутствии данного симптома 1 ошибки.
Симптом 3-й – существенные отличия в оценках соответствующих коэффициентов модели по 2 одинаковым частям уравнения наблюдения. Можно заметить некоторые отличия в оценках параметров, но они не столь существенные (табл. 3).
Таблица 3
Проверка на наличие 3 симптома 1 ошибки
|
Первая часть |
Вторая часть |
||||||
|
|
|
|
|
|
|
|
|
|
0,142 |
-2,680 |
0,621 |
292,109 |
0,233 |
-4,529 |
0,561 |
474,550 |
|
|
|
|
|
|
|
|
|
|
0,059 |
1,119 |
0,085 |
115,513 |
0,081 |
2,510 |
0,069 |
252,333 |
Источник: составлено автором.
Таблица 4
Проверка на наличие 2 ошибки.
|
|
|
|
|
|
|
Дробь Стьюдента |
3,89 |
-3,39 |
11,44 |
3,6 |
|
tкр |
2,003241 |
|||
Источник: составлено автором.
Таблица 5
Статистика Дарбина-Уотсона
|
M1 |
M2 |
M3 |
M4 |
M5 |
|
0-1,44 |
1,44-1,73 |
1,73-2,27 |
2,27-2,56 |
2,56-4 |
|
2,12 |
Источник: составлено автором.
Проверка на наличие 2-го вида ошибки – включение в функцию регрессии незначащей объясняющей переменной – показала ее отсутствие. Так как для всех параметров выполняется неравенство (Табл. 4): |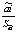 | > tкр. Все регрессоры и свободный член являются значимыми.
| > tкр. Все регрессоры и свободный член являются значимыми.
Ошибка 3-го вида – пропуск в функции регрессии значащей объясняющей переменной. По последствиям и симптомам она эквивалентна первой ошибке, чтобы убедиться в ее отсутствии проведем тест Дарбина-Уотсона.
DW = 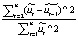 .
.
Вычисленное значение статистики DW для модели динамики оборота розничной торговли DW = 2,12, что близко к 2 и уже говорит об отсутствии корреляции случайных остатков. Количество наборов данных равняется n = 60, при этом количество регрессоров k = 3, тогда на уровне значимости 5 %, dl = 1,44 du = 1,73; 4-du = 2,27 и 4-dl = 2,56.
Как видно из Таблицы 5, статистика попадает в промежуток M3, что говорит об отсутствии автокорреляции. Следует отметить, что данное утверждение истинно при соблюдении других условий теоремы Гаусса-Маркова. При дальнейших расчетах была подтверждена его корректность.
В первую очередь, для получения оптимальных оценок параметров модели, следует правильно выбрать процедуру оценивания. Для применения метода наименьших квадратов (МНК) нужно, чтобы выполнялись все условия теоремы Гаусса-Маркова. Так как при их выполнении процедура оценивая будет генерировать оценки параметров, которые обладают двумя свойствами – несмещённости и эффективности: Е(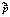 ) =
) = 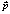 и Var(
и Var(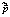 ) = min.
) = min.
Оценка качества спецификации (проверка справедливости выполнения первой предпосылки теоремы Гаусса-Маркова) проверяется процедурой R^2 и F теста. Невыполнение данного условия вызывает смещение оценок парметров.
Как уже было показано в Таблице 1, R^2 = 0,871, R^2 скорректированный же будет равняться 0,864, что говорит о сильной регрессии. Модель более чем на 86 % объясняется заданными факторами. Процедура F-теста поможет убедиться в статистической значимости и надежности коэффициента детерминации. Как видно из Таблицы 6 Fкр < Fнабл, что говорит о значимости коэффициента детерминации. Предложенная спецификация модели качественная.
Таблица 6
F тест
|
F кр |
2,769431 |
< |
126,1972 |
F набл |
Источник: составлено автором.
Вторая предпосылка теоремы Гаусса Маркова говорит о постоянстве дисперсий случайных остатков для всех наблюдений – гомоскедастичности: Var(u1) = Var(u2) =…= Var(ut) = 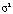 .
.
Если данное условие не будет выполняться, то оценки получатся неэффективными. Выполнение данного условия проверяется процедурой теста Голдфелда-Квандта.
Таблица 7
Тест Голдфелда-Квандта
|
GQ |
0,615354 |
< |
Fкр |
2,333484 |
|
1/GQ |
1,625082 |
< |
Источник: составлено автором.
Так как Fкр больше GQ и обратного показателя 1/GQ (Табл. 7), то мы принимаем гипотезу о гомоскедастичности случайных остатков и соответственно постоянстве дисперсий случайных остатков для всех наблюдений. 2-е условие теоремы Гаусса-Маркова соблюдается.
3-я предпосылка теоремы Гаусса-Маркова говорит о некоррелированности случайных остатков, т.е. об отсутствии связи между ними в любых наблюдениях: Cov(ui;uj) = 0 (при i ≠ j). В случае нарушения данного условия оценки получаются неэффективными.
Выполнение данного условия определяется проведением процедуры теста Дарбина-Уотсона, который был проведен ранее (Таблица 5). Статистика попадает в промежуток M3, что говорит об отсутствии автокорреляции и выполнении 3 условия теоремы Гаусса-Маркова.
4 предпосылка теоремы Гаусса-Маркова заключается в том, что случайное отклонение должно быть независимо от объясняющих переменных: Cov(ut;xtj) = 0. Данная предпосылка не нуждается в проверке, так как выполняется автоматически, потому что у нас нет статистики по случайным остаткам в силу их свойств, тогда как по регрессорам у нас имеются детерминированные значения.
Выполнение всех условий теоремы Гаусса-Маркова говорит об оптимальности полученных для модели оценок.
Для проверки адекватности используется точечный и интервальный прогноз. В данном случае контролирующая выборка будет содержать 57 наблюдений (95 % от общего числа наблюдений), контролирующая – 3 (5 %). Контролирующая выборка выбрана для последних трех наблюдений: октябрь, ноябрь, декабрь 2019 года. Так как это будет говорить о том, что нет смены тенденции (Таблица 8).
Таблица 8
Контролирующая выборка
|
y |
x1 |
x2 |
x3 |
|
|
окт.19 |
101,4 |
102,1 |
100,1 |
113,8 |
|
ноя.19 |
100,5 |
99,4 |
100,3 |
97,3 |
|
дек.19 |
118 |
134,5 |
100,4 |
104,8 |
Источник: составлено автором.
Для проверки модели на адекватность перенастроим рассматриваемую модель динамики розничной торговли по обучающей выборке (январь 2015 – сентябрь 2019). Полученные МНК-оценки представлены в таблице 9 ниже.
Таблица 9
Оценки параметров по обучающей выборке
|
0,169 |
-2,996 |
0,599 |
323,502 |
|
0,047 |
0,898 |
0,058 |
91,735 |
|
0,867 |
3,787 |
#Н/Д |
#Н/Д |
|
115,028 |
53,000 |
#Н/Д |
#Н/Д |
|
4948,773 |
760,060 |
#Н/Д |
#Н/Д |
Источник: составлено автором.
Прогнозные значения эндогенной переменной представлены во втором столбике (Табл. 10), а в третьем указана допустимая погрешность прогноза (она вычисляется как разность y фактического от y прогнозного). Чтобы модель признавалась адекватной нужно, чтоб данные погрешности не превышали среднее квадратическое отклонение по обучающей выборке. Для всех трех значений из контролирующей выборки выполняется данное неравенство, следовательно, модель можно назвать адекватной по результатам точечного прогнозирования.
Таблица 10
Точечный прогноз
|
y'1019 |
104,0367 |
2,63673 |
< |
3,78692 |
|
y'1119 |
99,03082 |
1,469183 |
< |
3,78692 |
|
y'1219 |
121,0485 |
3,048538 |
< |
3,78692 |
Источник: составлено автором.
Таблица 11
Интервальные прогнозы по контролирующей выборке
|
для октября 2019 г |
для ноября 2019 г. |
||||
|
q |
0,039277 |
q |
0,021469 |
q |
0,253314 |
|
S |
3,860574 |
S |
3,827355 |
S |
4,239514 |
|
tкр |
2,005746 |
tкр |
2,005746 |
tкр |
2,005746 |
|
y'-1019 |
96,2934 |
y'-1119 |
91,35412 |
y'-1219 |
112,5451 |
|
y'+1019 |
111,7801 |
y'+1119 |
106,7075 |
y'+1219 |
129,5519 |
|
y факт |
101,4 |
100,5 |
118 |
||
|
Вывод |
принадлежит интервалу |
принадлежит интервалу |
принадлежит интервалу |
||
Источник: составлено автором.
Для проведения интервального прогноза потребуется построение вектора х по контрольной выборке для каждого ее значения и матрицы х по обучающей выборке (нельзя забывать о включение в вектор x 1 и расширении единичным столбцом матрицы х, поскольку анализируемая модель является множественной регрессией).
Из таблицы 11 видно, что каждое фактическое значения значение наблюдаемого уровня динамики оборота розничной торговли из контролирующей выборки принадлежит соответствующим прогнозным интервалам (y'-; y'+). Следовательно, модель можно считать адекватной с 95 % вероятностью [3].
При проведении регрессионного анализа был простроена линейная модель зависимости динамики оборота розничной торговли от динамики номинальной заработной платы работников, динамики индекса потребительских цен и динамики импорта. Анализ наличия ошибок в спецификации показал отрицательный результат, исследование модели на соблюдение условий теоремы Гаусса-Маркова доказал, что оценки, полученные МНК являются оптимальными, а точечное и интервальное прогнозирование подтвердило адекватность полученной модели.
Следовательно, данная модель может использоваться для прогнозирования дальнейших показателей динамики оборота розничной торговли.