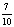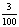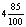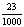В данном работе рассматривается проблема организации познавательной самостоятельности обучающихся пятых классов на уроках математики. Для решения указанной проблемы определены такие понятия как «самостоятельность», «познавательная самостоятельность», выделены их существенные свойства и приведена классификация. В статье на основе анализа литературы, обобщения педагогического опыта, изучения возрастных особенностей, наблюдения и эксперимента представлены технологии и их краткие характеристики. В статье приводятся конкретные тематические примеры организации самостоятельной познавательной деятельности посредством использования выявленных технологий (создание проблемной ситуации, работа с книгой и др.), эффективность которых доказана на практике.
Активно развивающийся социум предъявляет новые требования к системе образования, основной задачей которого в настоящее время является формирование у обучающихся способности к самостоятельной познавательной деятельности. Такая деятельность, кроме обучающих целей, несет в себе воспитательную, развивающую и другие функции. Обучающихся важно научить самостоятельно овладевать знаниями, применять их не только в учении, но и в практической деятельности. Естественно, познавательная самостоятельность не есть самоцель. Она – способ достижения многих предметных и метапредметных результатов обучения.
Проблема развития познавательной самостоятельности обучаемых затронута в многочисленных научно-педагогических исследованиях. Общая характеристика самостоятельной познавательной деятельности учащихся представлена в научных трудах – Е.Я. Голанта, М.И. Махмутова, Г.И. Саранцева и др., выделены виды самостоятельных работ – Б.П. Есипова, А.С. Лынды, И.В. Харитоновой и др., определены условия организации познавательной самостоятельности учащихся – М.А. Данилова, Б.П. Есипова, П.И. Пидкасистого, С.В. Напалкова, установлено содержание и уровни развития познавательной самостоятельности – Г.И. Саранцева, Т.И. Шамовой, С.В. Напалкова и др.
Однако, в процессе наблюдения за учебной деятельностью учащихся 5-х классов было выявлено, что школьникам не всегда под силу добывать знания самостоятельно и применять их в практической деятельности, им присущ репродуктивный стиль мышления, отсутствует умение анализировать и обобщать факты, сравнивать, отделять главное от второстепенного, соотносить условия учебной задачи с условиями ее достижения.
Необходимость решения указанных противоречий обусловливает значимость настоящего исследования по проблеме качественной организации познавательной самостоятельности учащихся на уроках математики. Актуальность подтверждается и требованиями федерального государственного образовательного стандарта, согласно которому самостоятельная познавательная деятельность учеников является приоритетной.
Цель исследования: определить эффективные технологии организации познавательной самостоятельности обучающихся 5-х классов и продемонстрировать возможность применения данных технологий на уроках математики.
Материал и методы исследования: исследовательская работа проведена на основе теоретических методов (изучение и анализ научно-методической, учебной и психолого-педагогической литературы) и эмпирических (наблюдение за участниками образовательного процесса, беседа с педагогическим составом школы, с преподавателями вуза, эксперимент). Исследование эффективности использования приемов организации познавательной самостоятельности проводилось на базе производственной практики МОУ «Лицей №43» города Саранск с использованием материально-технического и методического обеспечения школы.
Материалы исследования несут практическую значимость для педагогов математики в плане возможности организации самостоятельной деятельности обучающихся.
Результаты исследования и их обсуждение. Что же понимают под «самостоятельностью» и «познавательной самостоятельностью»? Анализ определений первого из понятий позволяет отметить единство взглядов почти всех исследователей в том, что самостоятельность есть внутренняя готовность личности к деятельности и интенсивное проявление этой готовности, обусловленное противоречием познающего субъекта и познаваемого объекта, заключающее в себе источники развития личности и преобразования окружающей действительности. Познавательная самостоятельность же определяется как качество личности, сочетающее в себе умение приобретать новые знания и творчески применять их в различных ситуациях. В такой трактовке отражено единство двух компонентов - мотивационного и процессуального. Первый отражает потребность в процессе познания, второй – знания данной предметной области, в частности математики, и приемы деятельности, способствующие осуществлению целенаправленного поиска [1].
Выделенные существенные свойства изучаемого понятия позволяют проводить различные классификации. В своем исследовании мы будем придерживаться классификации, согласно которой выделяются следующие виды познавательной самостоятельности [2]:
1) основанные на репродуктивном стиле обучения: подражание и воспроизведение школьниками действий учителя и его рассуждений;
2) требующие от учеников самостоятельного применения знаний, умений и навыков, полученных ранее под руководством учителя в обстоятельствах, подобных тем, в которых они формировались;
3) требующие от учеников самостоятельного применения знаний, умений и навыков, полученных ранее под руководством учителя в обстоятельствах, подобных тем, в которых они формировались, но в условиях, отличающихся от тех, которые имели место при формировании знаний, умений и навыков, применяемых школьниками в ходе выполнения конкретной задачи;
4) творческие работы, требующее от учащихся применения самостоятельности в ходе выполнения задания, в постановке проблемы и поиска сути ее решения, самостоятельного проведения необходимых исследований, самостоятельного получения заключения.
Конечно же, элементы познавательной самостоятельности начинают формировать в начальной школе, а в 5 классе учитель продолжает этот процесс. В основном, учащимся этого возраста присущ образный, конкретно-индуктивный стиль мышления, развито воображение. Поэтому они с удовольствием включаются в творческие процессы. Но именно в этом возрасте нужно формировать дедуктивное мышление, закладывать основы теоретического мышления [3, c. 127–149]. Изучение математики как нельзя лучше способствует достижению указанных целей.
Учитывая сказанное, охарактеризуем технологии организации познавательной самостоятельности обучающихся, которые на наш взгляд целесообразно применять на уроках математики в 5-х классах.
1. Технология привлечения жизненного опыта учащихся. Значительную роль в усвоении материала играют работы практического характера. Как показывает практика, школьники зачастую запоминают только то, над чем потрудились их руки, например, рисовали, чертили, вырезали или раскрашивали – это и служит опорой их памяти. Такой вид деятельности, как обучающее практическое занятие, является творческим для учащихся. В процессе выполнения задания и обобщения результатов, учащиеся приходят к новому математическому занятию. Результатом работы является внутренний продукт практической деятельности самих учащихся, а неполученные знания в виде готовой информации.
2. Технология самостоятельной работы с учебной литературой. Здесь можно выделить следующие наиболее распространенные виды работы с учебником: чтение текста про себя, чтение текста вслух; воспроизведение содержания прочитанного текста; анализ прочитанного текста и разбиение его на смысловые части, выделение главного (в начале с помощью учителя, потом самостоятельно); составление плана прочитанного; работа с иллюстрациями; работа над понятием, термином; составление конспекта, схемы, таблицы, графика на основе изученного материала; работа с оглавлением и предметным указателем [4].
3. Технология создания проблемной ситуации, в процессе которой сочетаются поисковая деятельность учащихся с усвоением знаний. Они возникают тогда, когда перед учащимися поставлена познавательная задача, которую они не могут решить сразу. Для того, чтобы её решить, ответить на возникший вопрос, учащимся необходимо приложить определённые усилия, провести наблюдения, сравнить полученные данные, проанализировать их и сделать соответствующий вывод [5].
4. Технология применения задач с избыточными данными. Решение задач данного типа позволяет выявить, как учащиеся из совокупности данных им величин выделяют именно те, которые представляют собой систему отношений математических величин и являются необходимыми и достаточными для решения задачи [6]. Это развивает у учащихся умения мыслить, рассуждать, исследовать и сравнивать, стоить логическую цепь рассуждений, выделять проблему и выбирать наиболее эффективные пути решения, что направлено на развитие познавательной самостоятельности [7].
5. Технология составления математических задач. Данный процесс можно организовать под руководством учителя или без его помощи, возможна групповая работа, где учащиеся выполняют ряд действий, операций. Данная организация деятельности выражает активное отношение учащихся к овладению знаниями, служит стимулом показать свои знания не только в области математики, но и в других аспектах жизни.
6. Игровые технологии. Игровая деятельность способствует внутренней мотивации к учению, формированию устойчивого интереса к углублённому изучению данного предмета, тем самым повышается уровень познавательной самостоятельности учащихся. Отметим, что урок может построен не полностью в форме игры, а с включением каких-либо игровых моментов, тем самым процесс обучения становится более интересным и занимательным, у школьников создается активное рабочее настроение.
Так, при изучении темы «Представление десятичных дробей» в 5 классе, для введения новой формы записи дробных чисел рационально использовать технологию создания проблемной ситуации. Учащимся предлагается несколько обыкновенных дробей, которые необходимо записать в новой форме. Разрешить возникшее у них затруднение поможет самостоятельна работа с карточками [8].
КАРТОЧКА № 1. Заполните пропуски в карточке и сформулируйте алгоритм перевода дробных чисел в десятичные дроби
|
Дробь |
Целая часть |
Количество нулей в знаменателе |
Количество цифр после запятой |
Десятичная дробь |
|
|
0 |
1 |
1 |
0, 7 |
|
|
0 |
2 |
2 |
0, . . |
|
|
4 |
4, . . |
||
|
|
0, . . . |
Технология выполнения данного задания: учащиеся самостоятельно, без помощи учителя, работая в микрогруппах, проводят наблюдение, сравнение, анализ, и на основе этого делают соответствующие выводы. Исходя из выявленных закономерностей, они формулируют алгоритм записи дробных чисел в виде десятичных дробей.
Также, для открытия правила чтения десятичных дробей можно использовать технологию работы с книгой, т.е. учащимся предлагается изучить самостоятельно теоретический материал учебника про себя и на основе изученного материала сформулировать правило чтения десятичных дробей, заполнив пропуски в утверждении, представленном на слайде презентации. Но до того как сформулировать правило, учащимся необходимо ответить на вопросы по прочитанному тексту. Вопросы могут быть следующие:
1. На чем основано чтение десятичных дробей?
2. Какие выделяют разряды десятичной дроби?
3. При чтении десятичной дроби, какую часть десятичной дроби сначала называют?
4. Какое слово необходимо добавить после чтения целой части десятичной дроби?
5. Для чего нужно определять название последнего разряда?
Заключение. В процессе изучения проблемы, заявленной в данном исследовании, мы определили эффективные технологии организации познавательной самостоятельности обучающихся 5-х классов и продемонстрировали возможность их использования на уроках математики. Представленные технологии действительно позволяют педагогу организовать и активизировать познавательную деятельность учащихся, что является очень важным в условиях «инновационного обучения». Немаловажно, что использование указанных приемов эффективно способствует развитию различных типов мышления учащихся, развитию устной речи, включает учащихся в поисковую, творческую деятельность, способствует повышению качества математической подготовки учащихся.