Scientific journal

Название журнала на английском

В статье рассматривается различные методы решения функциональных уравнений и неравенств. А также приведены решение задач относительно композиции функции. Такие задачи мало рассматриваются в школьном курсе математики, а часто встречаются в заданиях математической олимпиады. Приведены анализ применения разлияных методов решения функциональных уравнений и неравенств. Задача этой работы обеспечить более полное раскрытие применения функционального метода к решению уравнений и неравенств, от простых до сложных.

Функциональный метод решения уравнений и неравенств позволяет сделать более осмысленным их изучение. Свойства функции, геометрические образы необходимо широко использовать при изучении уравнений и неравенств. Решение уравнений и неравенств, отражающееся на функциональный метод, достаточно нетрадиционно и является творческой задачей.

а) Задачи относительно композиции функции.

Задача 1. Если 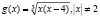. Найти значение выражения .

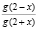Решение. Функция g(x) определена на всей числовой оси: х∈(-∞; + ∞).

Напмшем композиции функции , :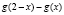

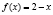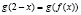, и функции , ,

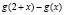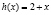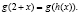
Тогда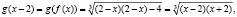

.

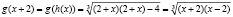Следовательно, значение выражения 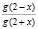при x ≠ 2 равно: .

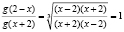Задача 2. Дано функция 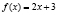. Найти ,

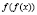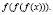
Решение. Имеем: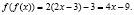

А композиции функции f(x) = 3-2x и f(f(x))=g(x) пишем в виде:

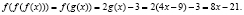
Задача 3. Пусть 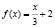. Вычислить значение функции 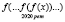при х = 4.

Решение. Для функции 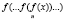получим следующью гипотезу:

при n = 1: .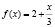

при n = 2: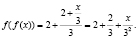

при n = 3: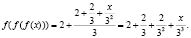

…………………………………………………………….

при n: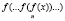

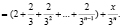
Эту гипотезу доказываем методом математической индукцией.

При n = 1 имеет место 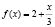. Пусть при n = k гипотеза верна, т.е.

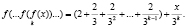
Теперь доказываем, что при случае n = k + 1. Действительно, имеем:

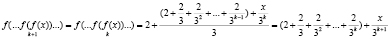
Таким образом, гипотеза верна при любом натуральном значении n:

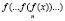
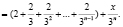
При n = 2020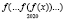

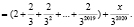
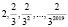– безконечно убывающая геометрическая прогрессия с знаменателем 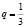, ее сумма равна: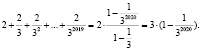

Тогда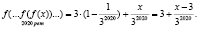

При x = 4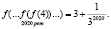

б) Различные методы решение функциональных уравнении и неравенств.

Под функциональным методом решения уравнений и неравенств понимают метод решения, опирающийся на использование свойство функций, входящих в уравнении и неравенство. Изучение роли функционального метода решения уравнений и неравенств является целью этой работы.

Функциональный метод используется:

1) В обосновании классических методов решения уравнений и неравенств (теорем равносильности, методов интервалов);

2) используется для решения задач, которые другими методами решить нельзя;

3) некоторые задачи можно решить разными способами, но более рациональным методом является функциональный;

4) при решении уравнений и неравенств, которые являются математической моделью других задач: нахождение области определения, множества значений функций, нахождение интервалов монотонности.

Большинство функциональных уравнений могут быть не определены специальной функцией, то есть класса функций, которые обладают обобщенными свойствами. Например, уравнение f(x + 1) = f(x) – характеризует класс функций, период которых равен 1, а уравнение f(1 + x) = f(1-x) – класс симметричных функций по отношению к прямой x = 1. Особое место в теории функциональных уравнений занимают дифференциальные уравнения. Показать некоторые методы решения функциональных уравнений.

Задача 4. Решить уравнение .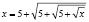

Решение. х > 5. Рассмотрим функцию 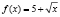. Тогда данное уравнение примет в виде функционального уравнения: .

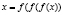Так как функция 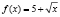возрастающая, то уравнение 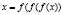равносильно уравнению x = f(x), т.е. уравнению 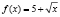= 0.

Решая этого уравнения, находим: .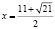

Задача 5. Найти всех непрерывные функций f(x), если .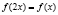

Решение. Сделаем замену х > 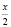, тогда: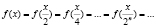

Так как функция f(x) непрерывная, то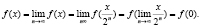

Значить, .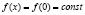

Задача 6. Найти всех дифференцируемых функций f(x), если

.

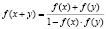Решение. Пусть х = у = 0, тогда 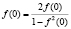, отсюда f(0) = 0.

Преобразуя данного уравнение (y = h), получим: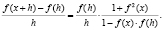

Учитывая, что 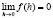, находим предел при h > 0:

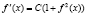, где С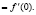

Интегрируем последнего уравнения: 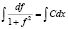, получим:

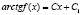, бyдан .

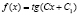Так как 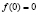, то С1 = 0 и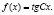

Задача 7. Решить уравнение .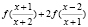

Решение. Выполняем следующие действия:

1) Замена 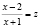, тогда ,

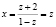2) Выражение х подставляем в данному уравнению:

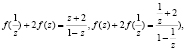
3) Заменяем z через :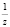

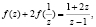
4) Таким образом получаем два уравнения:

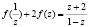и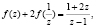

5) Умнажая первого уравнения на (-2), сложим на вторую уравнению:

Тогда, получим: 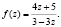Значит, искомая функция есть: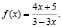

Задача 8. При положительных значении переменных x и y для функции f(x) имеет место равенство f(xy) = f(х) + f(у). Если 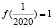, то найти f(2020).

Решение. По условию f(1·1) = f(1) + f(1) или 2f(1)=f (1). Значит, f(1) = 0. Для всех положительных х выполняется равенство:

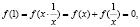тогда

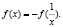
Следовательно, при x = 2020, получим: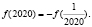

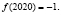
Задача 9. При всех рациональных значении x и y функция f(x) удовлетворяет условию 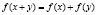. Известно,что 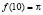. Найти 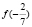табындар.

Решение. По условию 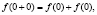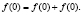Значить, 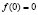и

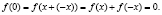Тогда, отсюда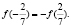

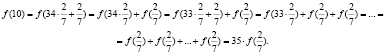
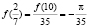, ал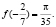

Задача 10. Дана функция 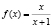. Решить неравенство .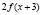

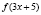Решение. 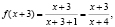Так как 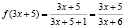, то данное неравенство примет вид: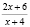 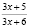, 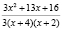< 0.

Так как неравенство 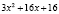> 0 имеет место при всех действительных значении х, то решение последнего неравенства будет промежуток .

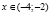Задача 11. Пусть 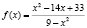, 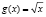. Решить неравенство .

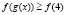Решение. 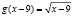, тогда .

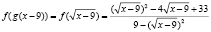Если 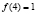, то неравенство 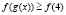примет вид:

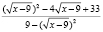≥ 1.

Обозначим, что 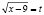, то t ≥ 0 и имеем систему неравенств:

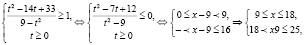
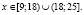
Таким образом, обобщенные методы задач относительно функциональной зависимости пока не сформулированы, очевидно, можно отнести функциональные уравнения и неравенства с использованием следующих индивидуальных методов и приемов:

– использовать непрерывность функций, устойчивость, монотонность, периодичность, парно-досоковые свойства;

– нули функции или метод неподвижных точек;

– дифференциальный метод, метод перехода на предельный;

– метод разницы;

– метод применительно к функционально заданным свойствам неизвестной функции;

– метод математической индукции;

– способность принимать большие или малые значения функции в какой-либо точке;

– метод рекурентных ошибок;

– метод замены переменных или выражений относительно аргумента;

– метод записи функции в виде суммирования четных и нечетных функций.

Известно, что обобщенные методы решения функциональных уравнений, не приводимые в дифференцирование и интеграцию, являются малыми. Функциональные уравнения часто встречаются при решении множества прикладных задач, при составлении расписания занятий, в системе управления ракетами и других практических задачах. Также решение функциональных уравнений и неравенств рекомендуется на Олимпиадах для школьников и студентов. От учащихся требуется во всякой конкретной задаче отвлечься от несущественных деталей и увидеть в ней общее функциональное содержание: найти реальные области изменения величин, выяснить характер их зависимости. Решение таких задач воспитывает:

- умение схематизировать;

- развивает интуицию;

- прививает навыки дедуктивного мышления;

- развивает творческие исследовательские способности.

Иначе говоря, способствует развитию математической культуры, играет большую роль для развития личности учащихся. То есть имеет большое педагогическое значение.