В настоящее время мировой туристический рынок характеризуется высокой степенью конкуренции, и специалист, работающий в сфере туризма и гостиничного бизнеса, должен быть готов к принятию решений в условиях неопределенной конкурентной среды [1]. Нечеткая марковская цепь является одной из моделей неопределенности, в которой сочетаются случайность и нечеткость, что в свою очередь приводит к появлению понятия нечеткой вероятности. В классической теории вероятность есть детерминированная характеристика возможности появления событий в определенных условиях. Вместе с тем, в реальной жизни эта возможность может неконтролируемым образом зависеть от совокупности условий, которые сами могут измениться. В этих случаях вероятность естественно описывать нечетким числом с функцией принадлежности, параметры которой оцениваются статистически по совокупности испытаний [2]. Нечеткие марковские процессы с дискретными состояниями удобно представлять и иллюстрировать с помощью нечеткой переходной матрицы и нечеткого графа состояний системы, поскольку система может прибывать в одном из n состояний и для каждого момента времени t необходимо задать n2 вероятностей перехода Pij [3-4].
В данной работе мы предлагаем рассмотрение представления нечетких целей Маркова в виде нечеткой переходной матрицы состояний с привлечением аппарата нечеткой математики. Предлагается математическая модель принятия решения на примере из сферы гостиничного бизнеса с привлечением однородных нечетких марковский цепей. Нечеткий случайный процесс будем называть нечеткой марковской цепью, если для каждого k-го шага случайная последовательность событий (состояний) S(0), S(1),…, S(k), нечеткая вероятность перехода из любого состояния Si в любое Sj не зависит от того, когда и как система пришла в состояние Sj. Начальное состояние S(0) может быть заданным заранее или случайным образом. Нечеткие вероятности цепи Маркова будем называть вероятности Pi(k) того, что после k-того шага (и до (k+1)-го) система S будет находится в состояние Si(i = 1, 2,…, n). Очевидно что для любого k:
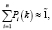(1)
где Pi(k) – нечеткие числа,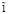 
– нечеткая единица, модальное значение которой равно 1.
Если начальное состояние системы S в точности известно S(0) = Si, то начальная вероятность Pi(0) = 1, а все остальные равны нулю.
Нечеткой вероятностью перехода (переходной вероятностью) на k-ом шаге из состояния Si в состояние Sj будем называть нечеткую условную вероятность того, что система S после k-го шага окажется в состоянии Sj при условии, что непосредственно перед этим (после (k-1)-го шага) она находилась в состоянии Si.
Поскольку система может пребывать в одном из n состояний, то для каждого момента времени t необходимо задать n2 нечетких вероятностей перехода Pij, которые удобно представить в виде следующей нечеткой матрицы:
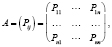(2)
где Pij – нечеткая вероятность перехода за один шаг из состояния Si в состояние Sj; Pij – нечеткая вероятность задержки в состояние Sj. Здесь Pij являются нечеткими гауссовыми числами с соответствующими функциями принадлежности:
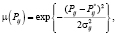где Pij – модальное значение (ядра) нечетких чисел; 
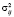– коэффициенты концентрации (носители). Матрица (2) называется нечеткой переходной или матрицей нечетких переходных вероятностей.
Если нечеткие переходные вероятности не зависят от номера шага (от времени), а зависят только от того, из какого состояния в какое осуществляется переход, то соответствующая нечеткая марковская цепь называется однородной.
Отметим некоторые особенности нечеткой матрицы, которые образуют переходные вероятности нечеткой однородной цепи Маркова:
- Каждая строка характеризует выбранное состояние системы, а её элементы представляют собой нечеткие вероятности всех возможных переходов за один шаг из выбранного (из i-го) состояния, в том числе переходов в самого себя.
- Элементы столбцов показывают нечеткие вероятности всех возможных переходов системы за один шаг в заданное (j-е) состояние (иначе говоря, строки характеризуют нечеткую вероятность перехода системы из состояния, столбец – в состояние).
- Сумма нечетких вероятностей каждой строки нечетко равна нечеткой единице, так как переходы образуют полную группу несовместимых событий:
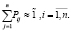(3)
- По главной диагонали матрицы нечетких переходных вероятностей стоят нечеткие вероятности того, что система не выйдет из состояния Si, и останется в нем.
Если для нечеткой однородной марковской цепи заданы нечеткое начальное распределение переходимых вероятностей (Pij), то нечеткие вероятности состояний системы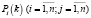 
определяюся рекуррентной формулой:
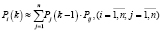(4)
с соответствующими функционалами принадлежности компонентов нечеткого решения задачи (4)
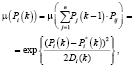(5)
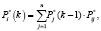
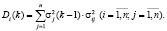
Построим математическую модель принятия решений в условиях неопределенности на примере из сферы гостиничного бизнеса с привлечением однородных нечетких марковских цепей.
Пример. Предприниматель намерен взять в аренду отель сроком на два года. Имеются два отеля А и В, которые расположены в разных районах города, но имеющих одинаковое количество комнат. Опыт эксплуатации этих отелей свидетельствует о том, что для них имеют место различные матрицы нечетных переходных вероятностей, соответствующих состояниям: занятость номеров более 90 % (состояние 1) и занятость номеров менее 90 % (состояние 2):
Отель А: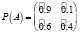 
, где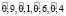 
– нечетные гауссовы числа с соответствующими функциями принадлежности
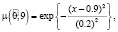
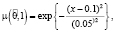
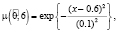
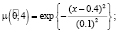
Отель В: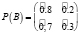 
, где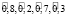 
– нечетные гауссовы числа с соответствующими функциями принадлежности
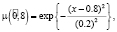
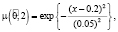
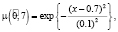
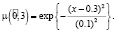
Нечеткие элементы матрицы перехода определены за годовой период эксплуатации отелей.
Требуется:
1. Найти нечеткие вероятности состояний для каждого отеля после двухлетней эксплуатации, если в начальном состоянии занятость номеров более 90 % (P1(0) = 1, P2(0) = 0);
2. Определить отель, который является более предпочтительным для взятия предпринимателем в аренду на два года.
Решение. Используя матрицу нечетких переходных вероятностей, определим нечеткие вероятности состояний Pi(k) после первого шага (после первого года эксплуатации отеля А) по формулам (4)-(5):
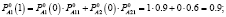
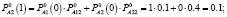
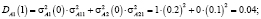
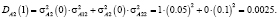
Таким образом, после первого года эксплуатации, отель А будет находится в состоянии 1 с нечеткой вероятностью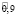 
и в состоянии 2 с вероятностью 
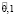с соответствующими функциями принадлежности:
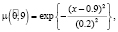
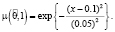
Определим нечеткие вероятности состояний после второго года эксплуатации отеля А:
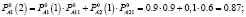
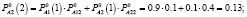
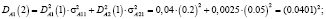
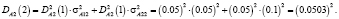
Таким образом, после второго года эксплуатации, отель А будет находиться в состоянии 1 с нечеткой вероятностью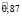 
и в состоянии 2 с вероятностью 
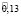с соответствующими функциями принадлежности:
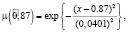
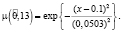
Аналогично определим нечеткие вероятности состояний Pi(k) после двух шагов (после двух лет эксплуатации отеля В):
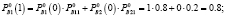
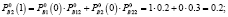
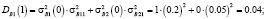
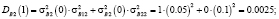
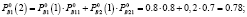
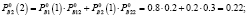
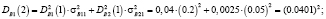
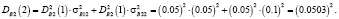
Таким образом, после второго года эксплуатации отель В будет находиться в состоянии 1 с нечеткой вероятностью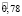 
и в состоянии 2 с вероятностью 
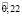с соответствующими функциями принадлежности:
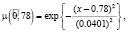
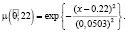
Сравним полученные нечеткие вероятности:
1) Численные значения коэффициентов концентрации совпадают;
2) Для модальных значений выполняются следующие неравенства:
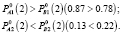
Таким образом, для предпринимателя предпочтительней является взятие в аренду на два года отеля А.
Выводы. В данной работе представлено рассмотрение основных понятий теории однородных нечетких цепей Маркова с привлечением нечеткой математики. Предложена математическая модель принятия решения на примере из сферы гостиничного бизнеса с привлечением однородных нечетких марковских цепей.