В статье рассматриваются теоретические и практические расчеты для решения задач практического назначения с помощью регрессионного анализа. Регрессионный анализ – метод моделирования измеряемых данных и исследование их свойств. Данные для анализа состоят из пар значений зависимой переменной и независимой переменной [1, 2].
Регрессионный анализ позволяет обнаружить скрытые зависимости и представить их в виде математических выражений. Основные цели регрессионного анализа: управление, предсказание, объяснение [3].
С помощью регрессионного анализа можно исследовать: эффективность работы организации, успеваемость школьника (студента), уровень жизни населения РФ (по городам), уровень загрязнения окружающей среды.
Главное достоинство регрессионного анализа в том, что мы получаем качественную модель с адекватным прогнозом, затратив при этом минимум времени.
Задачами регрессионного анализа является: установление формы зависимости, определение функции регрессии и оценка неизвестных значений.
Решение задач основывается на анализе статистических данных, в которых всегда присутствуют определённые отклонения (ошибки). Поэтому существуют специальные методы оценки как уравнения регрессии в целом, так и отдельных ее параметров.
Парная регрессия – уравнение связи двух переменных y и x: y = f(x), где y – результативный признак; x – признак-фактор.
Уравнение линейной регрессии (1).
y = a + bx. (1)
Построение уравнения регрессии сводится к минимизации суммы квадратов отклонения фактических значений результативного признака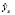 
от теоретической y (2).
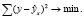(2)
Далее, вычислим значения a и b решив систему линейных уравнений 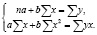(3).
(3)
Решение системы линейных уравнений (3) соответствует 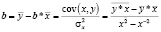(4).
(4)
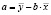
Тесноту связей оценивает коэффициент парной корреляции rxy в интервале –1 ≤ rxy ≤ 1.
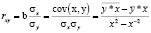(5)
Средняя ошибка аппроксимации, даёт оценку качества построенной модели:
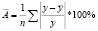(6)
Fфакт определяется, как соотношение факторной и остаточной дисперсии, рассчитывается по формуле 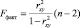(7).
(7)
Fтабл – это возможное значение под влиянием случайных факторов.
Если Fтабл < Fфакт, то гипотеза признаётся, как статистически значима (надежна).
Если Fтабл > Fфакт, то гипотеза характеризуется, как ненадежная (незначимая).
Перейдём к решению задачи.
Решим задачу с помощью регрессионного анализа, используя теоретические данные таблице, где y – заработная плата, x – расходы.
В ходе решения будет использовать формула (1) и (4):
;
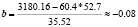a = 60.4 + 0.08•52.7 ≈ 64.62.
Уравнение регрессии выглядит следующим образом (8).
y = 64.62 – 0.08x. (8)
Из уравнения (8) видно: при увеличении заработной платы на одну условную единицу (руб.) доля расходов снижается на 0.08 %.
Рассчитаем линейный коэффициент парной корреляции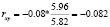 
, в ходе решения используем формулу (5).
Исходя из полученного результата, можно говорить о тесноте связи между переменными x и y, при rxy = –0.082 – связь умеренная, обратная.
Исходные данные
|
y |
x |
xy |
x^2 |
y^2 |
|
|
1 |
70,5 |
44,2 |
3116,1 |
4970,25 |
1953,64 |
|
2 |
65,8 |
52,1 |
3428,18 |
4329,64 |
2714,41 |
|
3 |
62,3 |
60 |
3738 |
3881,29 |
3600 |
|
4 |
58,2 |
62,4 |
3631,68 |
3387,24 |
3893,76 |
|
5 |
56 |
47,2 |
2643,2 |
3136 |
2227,84 |
|
6 |
49,8 |
50,7 |
2524,86 |
2480,04 |
2570,49 |
|
Итого |
362,6 |
316,6 |
19082,02 |
22184,46 |
16960,14 |
|
Ср.знач.(Итого/n) |
60,4 |
52,7 |
3180,16 |
3697,41 |
2826,69 |
|
S |
5,82 |
5,96 |
|||
|
S^2 |
33,87 |
35,52 |
Найдем среднюю ошибку аппроксимации, в ходе решения будем использовать формулу (6):
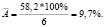
В среднем расчетные значения отклоняются от фактических на 9,7 %.
Для начала найдем коэффициент детерминации: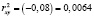 
.
Вычислим Fфакт используя формулу (7):
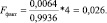
Выявленное значение указывает на то, что необходимо принять статистическую незначимость параметров уравнения.
Таким образом, проанализировав результаты исследования, мы научились решать задачи и убедились в том, что регрессионный анализ дает возможность оценить степень связи между переменными путем вычисления предполагаемого значения переменной на основании нескольких известных значений.