Научный руководитель: Коган Л.П.
Предложена методика исследования свойств функций вещественной переменной, заданных при помощи сложно вычисляемых операторов. Исследование проводится путем перехода с вещественной оси на комплексную плоскость и анализа поведения мнимой части натурального логарифма от исследуемой функции.
В данной работе анализируется возможность изучения свойств функции вещественной переменной, заданной в виде сложного математического оператора. Пусть искомая функция f(x) записана таким образом, что ее значения могут быть рассчитаны только численно. Например, пусть f(x) задана в виде обратного преобразования Фурье
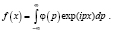 (1)
(1)
а) б)
в) г)
д)
Рис. 1
Если подынтегральный множитель φ(p) является достаточно сложным для интегрирования (например, он является комбинацией нескольких специальных функций), то интеграл (1) не удается вычислить в аналитическом виде. При этом часто становится принципиально важно выяснить свойства f(x). В частности, во многих случаях возникает вопрос о наличии составе f(x) слагаемого, которое является пренебрежимо малым в области малых значений аргумента, но определяет вид этой функции при больших x. Кроме того, принципиально важным является исследование правой части (1) на наличие малого гармонического слагаемого, что может говорить о резонансных свойствах исследуемой функции, а также изучение вопроса о возможности экспоненциального возрастания или, наоборот, затухания (1) при x→∞.
Для решения такой задачи выполним аналитическое продолжение f(x) на плоскость комплексной переменной z = x + iy, после чего рассмотрим мнимую часть натурального логарифма [1]:
s(x, y) = Im{ln[f(z)]}. (2)
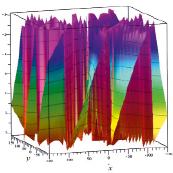
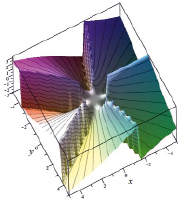
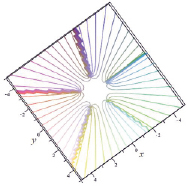
На рис. 1 показан вид зависимости s(x, y), отвечающей функции.
f(x) = x5 + 10-10x10. (3)
Отметим, что принципиально важной особенностью построения всех приводимых далее рисунков является конечность числа точек, используемых программой-графопостроителем. Благодаря чему стремится к нулю вероятность того, что одна из таких точек в точности совпадет с точкой, где f(z) = 0. Данное обстоятельство позволяет исследовать свойства s(x, y) несмотря на то, что в некоторых точках рассматриваемой декартовой области значения функции ln[f(z)] →∞.
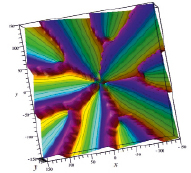
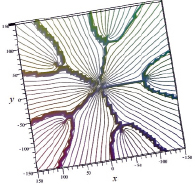
На рис. 1а и 1б изображен общий вид (в боковой и верхней проекциях) двумерного графика для s(x, y); на рис. 1в приведен более удобный для анализа вид сверху для линий уровня для всего рис. 1а. На рис. 1г и 1д приведен вид сверху для линий уровня центральной части рис. 1а. Как следует из свойств натурального логарифма от комплексной функции, при обходе вокруг точки, в которой f(z) = 0, значение Im{ln[f(z)]} меняется на 2π. Из анализа рис. 1г и 1д следует, что в области относительно малых значений |{Re, Im}z| ≤ 5, где второе слагаемое в правой части (5) (при замене x на z) по модулю является по пренебрежимо меньшим первого, имеет место только 5 корней уравнения f(z) = 0. Каждому такому корню отвечает разрез на плоскости комплексной переменной, который (с учетом однолистности изображенных графиков) приводит к появлению линии максимума, на которой Im{ln[f(z)]} = 2π. Любая подобная линия (своего рода «горный хребет» на рис. 1) начинается в той точке, где f(z) = 0, и далее уходит в бесконечность. Поскольку при 50 ≤ |z| ≤ 150 указанное второе слагаемое по модулю становится величиной порядка (а затем и много большим) первого, то в этой области имеют место остальные 5 корней данного уравнения f(z) = 0, см. рис. 1б и 1в. Отвечающие им дополнительные разрезы (см. пять точек ветвления «горных хребтов» на рис. 1б и 1в) в области больших значений |z|) также уходят в бесконечность.
По аналогии может быть исследована функция
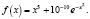 (4)
(4)
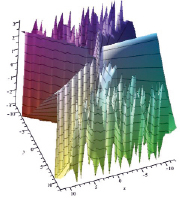
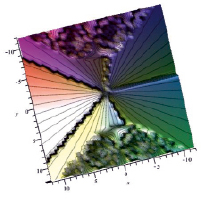
а) б)
Рис. 2
На рис. 2а и 2б приведены вид в боковой проекции и вид сверху для зависимости (2), отвечающей (4) при замене f(x) на f(z = x + iy). Как видно из этих рисунков, в области относительно малых значений |{Im}z| ≤ 5 зависимость s(x, y) практически та же, что и на рис. 1г и 1д. (При этом имеют место только пять разрезов, связанных с неоднозначностью мнимой части логарифма от x5 при обходе вокруг точки нуля.) Следовательно, в этой области влиянием второго слагаемого в (4) можем пренебречь. В то же время в области |{Im}z| ≥ 6.5 возникают множественные «пики», соответствующие новым точкам, в которых f(z) = 0, см. рис. 2б. Такого рода структура функции s(x, y) является маркером наличия экспоненциального (или гармонического) слагаемого для функции f(x).
Следовательно, наличие малого экспоненциального слагаемого при переходе в комплексную область приводит к существенно иному виду функции s(x, y), чем это имеет место при прибавлении малого степенного слагаемого. Этот факт может быть полезен при анализе поведения на вещественной оси функции, заданной с помощью сложно вычисляемого оператора.
Таким образом, приходим к выводу, что предлагаемая методика позволяет эффективно анализировать свойства функций, заданных в форме трудно вычисляемых операторов.

