В статье рассматривается диалектическое представление о понятие пространства в материалистическом мире, т.е. естественное представление о пространстве и времени.
Проведен анализ естественнонаучного представления о пространстве-времени. Здесь основными были представления о пространстве и времени как о каких-то внешних условиях бытия, в которые помещена материя и которые сохранились бы, если бы даже материя исчезла. Такой взгляд позволил сформулировать концепцию абсолютного пространства и времени, получившую свою наиболее отчетливую формулировку в работе И. Ньютона «Математические начала натуральной философии». В нем были сформулированы основные законы движения и дано определение пространства – времени, места и движения. В работе изложены факты четырехмерного пространство Г. Минковского, как геометрическую интерпретацию специальной теории относительности. Наглядно иллюстрировано координатно-геометрический критерий относительной и абсолютной одновременности событий.
Понятие пространства возникло на основе наблюдения и практического использования объектов, их объема и протяженности. А понятие времени возникло на основе восприятия человеком смены событии, последовательной смены состояний предметов и круговорота различных процессов.
Современное понимание пространства и времени было сформулировано в теории относительности А. Эйнштейна, по-новому интерпретировавшей реляционную концепцию пространства и времени и давшей ей естественнонаучное обоснование.
Эйнштейн сделал вывод, что длительность промежутка времени между двумя событиями и величина расстояния между двумя точками пространства должны быть разными в разных инерциальных системах координат, движущихся относительно друг друга.
80 лет назад Герман Минковский предложил геометрическую интерпретацию специальной теории относительности. В наши дни знакомство с теорией относительности стало необходимым элементом общего образования, однако преподавание и понимание этой теории до сих пор затруднено тем, что ее математическое описание находится в противоречии с теми представлениями о пространстве и времени, которые базируются непосредственно на чувственных восприятиях и закрепляются в процессе изучения классической физики. Чтобы понять геометрию Минковского надо изучить представление о псевдоевклидовом пространстве. Прежде всего, требуется понятие абстрактного линейного пространства и его разновидности – евклидова пространства, умение различать линейные и метрические свойства пространства.
Понятие одновременности не допускало различных толкований в классической физике: если отсчет времени не зависит от выбора пространственной системы координат, то события, совершающиеся в один и тот же момент времени в какой-либо координатной системе, являются одновременными и во всякой другой системе. Одновременность, таким образом, выступала в качестве абсолютной характеристики событий, не зависящей от выбора системы координат.
В теории относительности понятие одновременности событий перестает быть однозначным, и модель мира Минковского дает этому простое объяснение.
Инерциальным системам координат ОХ и О’Х’ в одномерном чувственно воспринимаемом пространстве, движущимся относительно друг друга, соответствуют в псевдоевклидовой плоскости мирового пространства ортонормированные системы координат OXY и О'Х'У' с различными направлениями осей OY и O'Y'. Удобно рассматривать системы, имеющие общее начало координат О. В каждой ортонормированной системе координат на псевдоевклидовой плоскости линия одновременности (прямая, на которой все точки имеют одинаковое значение ординаты у = ct) перпендикулярна к оси ординат. На рисунке изображены три такие системы: OXY, OX'Y', OXY''. На осях ординат этих систем выберем три точки А, В, С, имеющие одно и то же значение ординаты y = yA в системе OXY, т.е. одновременные в не штрихованной координатной системе. Эти же точки имеют уже не одинаковые, а различные значения ординаты в штрихованной координатной системе OX'Y'.
Проведем через точки А, В, С линии одновременности системы OX'Y': у' = у'в, АА', СС'. Пересечения их с осью OY’ указывают значения ординаты у' событий А, В, С в штрихованной координатной системе и последовательность событий во времени с точки зрения этой системы: В → А → С. В дважды штрихованной системе координат OXY'' линии одновременности у'' = y''в, АА'', ВВ'' показывают, что события А, В, С сменяют друг друга в иной последовательности, а именно: С → А → В.
Для наблюдателя, связанного с мировой прямой OY', цепочка событий В → А → С обозначает переход от прошлого к будущему (возрастание ординаты y'), а для наблюдателя, связанного с мировой прямой OY'', та же последовательность событий В → А → С обозначает переход от будущего к прошлому (убывание ординаты у'').
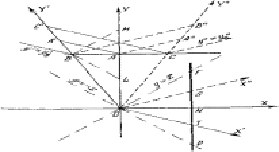
Теория относительности не отрицает абсолютного различия между прошлым и будущим, а напротив, формулирует четкие условия возможности такого различения, которые просто и наглядно интерпретируются в модели мира Минковского. Для того чтобы две мировые точки А и В могли быть одновременными в какой-либо ортонормированной системе координат OXY псевдоевклидовой плоскости, они должны лежать на перпендикуляре к оси ординат этой системы. И поскольку ось OY принадлежит мнимым секторам, прямая, соединяющая точки А и В, должна принадлежать вещественным секторам. Любая ось OY может быть повернута как в положительную, так и в отрицательную сторону, поскольку угол между любым не изотропным вектором верхнего сектора и каждой изотропной прямой, ограничивающей сектор, бесконечно велик. Поэтому всегда найдутся такие координатные системы OX'Y' и OXY'', у которых оси ОY' и OY'' расположены по разные стороны от оси OY. Если вектор 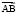 имеет отрицательную проекцию на ось OY', то мировая точка В является более ранней в системе OX'Y', чем точка А. При этом проекция вектора
имеет отрицательную проекцию на ось OY', то мировая точка В является более ранней в системе OX'Y', чем точка А. При этом проекция вектора 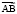 на ось OY'', отклоненную в другую сторону от OY, окажется положительной, и мировая точка В будет более поздней в системе OXY'', чем точка А. Зависимость порядка следования событий от выбора координатной системы возможна лишь для таких мировых точек А и В, расстояние между которыми выражается вещественным числом (вектор
на ось OY'', отклоненную в другую сторону от OY, окажется положительной, и мировая точка В будет более поздней в системе OXY'', чем точка А. Зависимость порядка следования событий от выбора координатной системы возможна лишь для таких мировых точек А и В, расстояние между которыми выражается вещественным числом (вектор 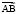 принадлежит вещественному сектору).
принадлежит вещественному сектору).
Если же мировые точки Р и F таковы, что расстояние между ними выражается мнимым числом (вектор 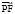 принадлежит мнимому сектору) или равно нулю (точки лежат на одной изотропной прямой), то вектор
принадлежит мнимому сектору) или равно нулю (точки лежат на одной изотропной прямой), то вектор 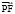 не может быть перпендикулярным к какой-либо прямой мнимого сектора. Следовательно, не существует такой системы координат OXY, в которой мировые точки Р и F могли бы быть одновременными. Пусть в какой-нибудь координатной системе точка Р является более ранней, чем точка F (вектор
не может быть перпендикулярным к какой-либо прямой мнимого сектора. Следовательно, не существует такой системы координат OXY, в которой мировые точки Р и F могли бы быть одновременными. Пусть в какой-нибудь координатной системе точка Р является более ранней, чем точка F (вектор 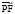 принадлежит верхнему сектору или одной из ограничивающих его изотропных прямых). Тогда проекция вектора
принадлежит верхнему сектору или одной из ограничивающих его изотропных прямых). Тогда проекция вектора 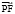 на любое не изотропное направление верхнего сектора будет положительной и, значит, в любой координатной системе событие F будет более поздним, чем событие Р. На рисунке все точки верхнего сектора, исходящего из точки О, включая ограничивающие его изотропные прямые у = х и у = –х, находятся в области абсолютного будущего по отношению к точке О, а все точки нижнего сектора вместе с ограничивающими его изотропными прямыми – в области абсолютного прошлого. Из каждой точки псевдоевклидовой плоскости исходят два сектора: сектор абсолютного прошлого и сектор абсолютного будущего. Как отмечено выше, вектор, касательный к любой мировой линии в любой ее точке и направленный в сторону роста мировой линии, принадлежит верхнему сектору. Поэтому какую бы точку на мировой линии мы ни выбрали, вся мировая линия не выйдет за пределы мнимых секторов, имеющих вершину в выбранной точке. А это значит, что на любой мировой линии различие между прошедшим и будущим не может зависеть от выбора координатной системы и в этом смысле абсолютно. Для точек любой изотропной прямой различие между прошедшим и будущим тоже абсолютно.
на любое не изотропное направление верхнего сектора будет положительной и, значит, в любой координатной системе событие F будет более поздним, чем событие Р. На рисунке все точки верхнего сектора, исходящего из точки О, включая ограничивающие его изотропные прямые у = х и у = –х, находятся в области абсолютного будущего по отношению к точке О, а все точки нижнего сектора вместе с ограничивающими его изотропными прямыми – в области абсолютного прошлого. Из каждой точки псевдоевклидовой плоскости исходят два сектора: сектор абсолютного прошлого и сектор абсолютного будущего. Как отмечено выше, вектор, касательный к любой мировой линии в любой ее точке и направленный в сторону роста мировой линии, принадлежит верхнему сектору. Поэтому какую бы точку на мировой линии мы ни выбрали, вся мировая линия не выйдет за пределы мнимых секторов, имеющих вершину в выбранной точке. А это значит, что на любой мировой линии различие между прошедшим и будущим не может зависеть от выбора координатной системы и в этом смысле абсолютно. Для точек любой изотропной прямой различие между прошедшим и будущим тоже абсолютно.
Согласие обоих критериев может нарушиться, когда речь идет о точках, не лежащих на одной мировой линии. На рисунке точки Р и F лежат на изотропных прямых у = –х и у = х, пересекающихся в точке О. Поэтому точка Р и все точки, расположенные ниже нее на прямой PF, являются абсолютно прошлыми по отношению к точке О. Точка F и все точки, расположенные выше нее на прямой PF, являются абсолютно будущими по отношению к точке О. Но любая внутренняя точка отрезка PF удалена от мировой точки О на расстояние, выражаемое вещественным числом. Поэтому для каждой внутренней точки отрезка PF найдется такая система координат, в которой эта точка одновременна точке О, и найдутся такие системы координат, в которых эта точка является либо более ранней, либо более поздней, чем точка О. Например, в координатной системе OXY мировой точке О одновременна точка N на прямой PF. В координатной системе OX'Y' точке О одновременна точка Т на прямой PF, а точка N является будущей. В координатной системе OXY'' точке О одновременна точка S на прямой PF, а точка N является прошлой. Это знакомая нам относительность одновременности, базирующаяся на координатно-геометрическом критерии. Другой же критерий, основанный на представлении о проявляющем процессе, не допускает такой многозначности временных отношений. По этому критерию независимо от выбора координатной системы возможно лишь одно из трех отношений: 1) мировая точка N проявляется вместе с точкой О; 2) точка N проявлена прежде точки О; 3) точка N проявится после точки О.
Каждый наблюдатель, несомненно, ощущает реальность границы между своим проявленным прошлым и непроявленным будущим. В любое мгновение своей жизни он переживает акт проявления и справедливо убежден, что в таком же положении находятся все другие наблюдатели и неодушевленные предметы. Какая же точка мировой линии PF проходит акт проявления вместе с точкой О? Здесь мы заменяем словом «вместе» слово «одновременно», поскольку стало уже привычным понимать одновременность в смысле координатного критерия. Если есть такие состояния мира, в которых существуют (проявлены) обе мировые точки О и N, и есть такие состояния мира, в которых не существует ни одна из них, но нет таких состояний, в которых одна из этих точек существовала бы, а другая не существовала, то мы скажем, что точки О и N проходят акт проявления вместе. Точки, проявляющиеся вместе, заслуживают названия абсолютно одновременных.
Координатно-геометрический критерий не допускает абсолютной одновременности. Поскольку все инерциальные системы координат в чувственно воспринимаемом пространстве равноправны и равноправны соответствующие им ортонормированные системы координат в псевдоевклидовом мировом пространстве, суждение об одновременности и разновременности мировых точек с позиций одной координатной системы столь же справедливо, как суждение с позиций любой другой системы, хотя бы эти суждения и противоречили друг другу. Раз не существует привилегированной (абсолютной) системы координат, то не может быть и абсолютной одновременности.
Но мы основываем понятие абсолютной одновременности не на координатно-геометрическом критерии и потому не вступаем в логическое противоречие с ним. Больше того, это понятие не вступает в противоречие и с экспериментальными основаниями теории относительности, поскольку экспериментирование с механическими и электромагнитными явлениями не позволяет обнаружить абсолютную одновременность. Предположим, что состояние наблюдателя, связанного с мировой прямой OF на рисунке, изображается мировой точкой А. Наблюдатель знает, что он находится на границе между проявленным и не проявленным и переживает в свой настоящий момент времени акт проявления. Но восприятию наблюдателя в этот момент недоступна мировая точка В на прямой OF', и потому он не может знать, проявляется ли она вместе с А, была ли проявлена раньше или будет проявлена позже. Мировая точка В окажется доступной восприятию наблюдателя, когда он будет перенесен ходом проявляющего процесса вдоль своей прямой в точку М, лежащую на одной изотропной прямой с точкой В. Но это уже не поможет решению интересующего его вопроса. Факт наблюдаемости точки В из точки М будет говорить лишь о том, что точка В проявлена раньше точки М, и ничего не скажет о соотношении моментов проявления точек В и А. Между тем вполне возможны физические эксперименты, позволяющие наблюдателю, связанному с мировой прямой OF, измерить координаты точки В в его координатной системе OXY. Предположим, что в мировой точке О, где встречаются мировые прямые OY и OF', наблюдатель из OF произвел установку некоторого отражающего устройства на материальной точке, соответствующей мировой прямой OY'. В последующие моменты времени наблюдатель организует излучение фотонов из мировых точек своей прямой OF таким образом, чтобы в каждом фотоне (серии фотонов) содержалась информация о том, в какой момент времени по часам наблюдателя произошло излучение. Спустя некоторое время наблюдатель на прямой OF начнет принимать отражения своих сигналов с прямой OF' и отмечать моменты приема сигналов. Располагая такими экспериментальными данными, наблюдатель будет рассуждать следующим образом. Если в его мировой точке М принято отражение сигнала, который был испущен t секунд тому назад, то это значит, что сигнал был послан из мировой точки L, отделенной от точки М отрезком длиной 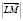 = ict. Отсюда можно найти ординату точки L.
= ict. Отсюда можно найти ординату точки L.
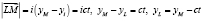 .
.
За время t световой сигнал прошел вдоль оси ОХ туда и назад расстояние 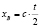 , определяющее абсциссу мировой точки В, отразившей сигнал. Ордината точки В равна
, определяющее абсциссу мировой точки В, отразившей сигнал. Ордината точки В равна 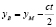 . На мировой прямой OY такую же ординату имеет точка А:
. На мировой прямой OY такую же ординату имеет точка А: 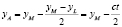 .
.
Откуда наблюдатель делает справедливое заключение, что его координатной системе мировая точка В одновременна точке А.
События, совершающиеся в настоящий момент времени, не вносят изменений в прошлое, не влияют на уже реализованные состояния мира, но будущие события формируются под влиянием прошлых и настоящих. Конечно, в известном смысле можно сказать, что будущее влияет на настоящее, поскольку, стремясь реализовать свои планы на будущее, мы подчиняем им свои действия в настоящем. Но, апеллируя к умственным способностям и творческим возможностям человека, мы выходим за рамки того круга явлений, в котором определяющую роль играют законы механики и электродинамики. Да и сам факт, что человек или иное живое существо может посредством целенаправленной деятельности (хотя бы и неосознанной) повлиять на ход будущих событий, направить их в то или иное русло, свидетельствует о том, что будущие события еще не реализованы, не проявлены, не существуют. Если бы будущие мировые точки были проявлены, как и прошлые, то жесткая предопределенность управляла бы развитием событий, и наше участие в жизни ограничивалось бы только пассивным просмотром существующих состояний мира в определенной последовательности. Лишилась бы почвы и смысла творческая активность, люди не имели бы возможности даже в малейшей степени быть творцами своего будущего.
Термодинамика характеризует положительное направление времени как такое спонтанное развертывание событий, при котором возрастает энтропия. Вот пара наглядных примеров процессов, протекающих с возрастанием энтропии. Перед началом биллиардной партии шары собраны в правильный треугольник, а после первого удара они беспорядочно рассеиваются по столу. Обратный ход времени применительно к этой ситуации выразился бы в том, что разбросанные шары должны собраться в исходный треугольник, что означало бы уменьшение энтропии системы. Другой пример. Вещество горящей сигареты рассыпается пеплом и рассеивается в окружающем воздухе в виде частиц дыма и газообразных продуктов горения (возрастание энтропии). Обратный ход времени выразился бы в обратной последовательности событий: не только рассеянные частицы собираются в целую сигарету, но и химические реакции протекают в обратном направлении, синтезируя из продуктов окисления крошки табака и вещество бумаги (уменьшение энтропии).
Для наблюдателя, состояние которого изображается на рисунке мировой точкой О, абсолютно будущими являются не только точки его собственной мировой линии, но и точки других мировых линий, находящиеся в верхнем секторе. Например, точка F и все более поздние точки на прямой PF являются абсолютно будущими по отношению к точке О. Но именно такие точки и не могут быть проявлены в тот момент, когда проявляющий фронт проходит через точку О, ибо он не выходит за пределы вещественного сектора. При любом допустимом расположении проявляющего фронта, проходящего через точку О, фронт необходимо пересечет отрезок PF в одной из его внутренних точек, которая и будет абсолютно одновременной точке О. Выше показано, что для любой внутренней точки отрезка PF найдется ортонормированная система координат, в которой эта точка одновременна точке О. Таким образом, абсолютная одновременность неизбежно примет форму относительной одновременности в какой-нибудь координатной системе, хотя мы и не можем узнать, в какой именно.

