Материалы Международной студенческой научной конференции

Студенческий научный форум 2025

• Авторы
• Файлы
• Литература

Губанова А.А. 1 Курган Н.С. 1 Синицын В.В. 1

---

1 ФГБОУ ВО «Донской государственный технический университет»

Статья в формате PDF

393 KB

1. Хайкин С. Нейронные сети. Полный курс. 2-е изд., испр. М.: Вильямс, 2008. 1103 с.

2. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы / Пер. с польск. И.Д. Рудинского. 2-е изд., стереотип. М.: Гор. линия – Телеком, 2013. 384 с.

3. Уорр К. Надежность нейронных сетей: укрепляем устойчивость ИИ к обману: практическое руководство. СПб.: Питер, 2021. 272 с.

4. Hinton G.E. et al. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. Journal of Machine Learning Research. 2012. Vol. 15. P. 1929–1958.

5. Метод решения проблемы переобучения в нейронных сетях. URL: https://habr.com/ru/company/wunderfund/blog/330814/Dropout.

Переобучение в машинном обучении в нейронных сетях (НС) представляет собой реальную проблему, которую в настоящее время нельзя полностью избежать. К факторам, образующим эффект переобучения можно отнести такие, как: 1) ограничение размера выборки обучающих данных, возможность их «очистки» от шумов; 2) сложность классификаторов; 3) сложность и многопараметричность обучающих алгоритмов.

Рассмотрим популярные стратегии, которые позволяют действенно устранять явление переобучения:

- стратегия сокращения – сокращает размер заключительных классификаторов в реляционном обучении, за счёт неприменения менее важных и неподходящих данных. Данная стратегия предотвращает явление переобучения и позволяет повысить точность классификаторов;

- стратегия ранней остановки- позволяет предотвратить переобучение путём прекращения обучения за счёт нахождения контрольной точки остановки обучения после определения того, что точность пробных данных престала улучшаться;

- стратегия расширения данных, заключающаяся в подавлении явления переобучения за счёт грамотной настройки гиперпараметров модели, её адекватной сбалансированностью между точностью и регулярностью обучения. Данная стратегия подразумевает более точно производить настройку параметров при достаточно больших объёмах данных;

- стратегия регуляризации, заключается в конечном выборе только «нужных» функций, влияющих на конечный результат;

- стратегия прореживания (отсева) наиболее популярная стратегия против переобучения в НС [1-3]. Рассмотрим её более детально.

Принцип стратегии прореживания заключается в том, что обучается не одна глубокая нейронная сеть, а целый набор, после чего берутся усреднённые результаты (рис. 1). Из сети выключаются нейроны с такой вероятностью P, что вероятность включения нейрона должна соответствовать условию d = 1 – P. Последнее означает, что исключение хотя бы одного из нейронов будет соответствовать обучению новой НС, а исключённый нейрон на входе всегда возвращает значение ноль [4,5].

Таким образом, распределение вероятностей 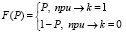(1):

, (1)

где k – вероятностные выходные значения.

Из рис. 2. видно, что слои x1…xn НС из N нейронов на каждой итерации этапа обучения можно считать как совокупность распределения Бернулли с вероятностью Р. Тогда на выходном слое мы получаем значение исключённых нейронов 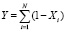(2):

, (2)

где Xi – вектор случайных величин.

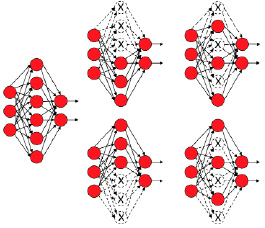
Рис. 1. Графическое представление метода прореживания

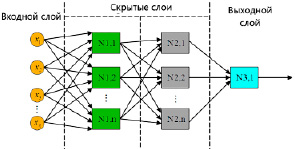
Рис. 2. Пример многослойной НС

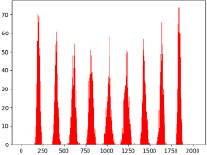
Рис. 3. Пример биномиального распределения

Исходя из (2) видно, что если слой состоит из 2048 нейронов и взяв P = 0,5, то видно, что 1024 из них будет выключено, т.е.:

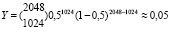
Получается, что вероятность отключения 1024 нейронов составляет 0,05. На рис. 3 представлено распределение значений вероятности выключения нейронов.

Библиографическая ссылка